Monte Carlo – Spielbank – Roulette – Zufallszahlen.

Das sind die Assoziationen, die einer der wichtigsten Methoden der Computersimulation den Namen gaben. Mit Hilfe von Zufallszahlen lassen sich im Rechner eine Vielzahl physikalischer Phänomene simulieren. Insbesondere sind diese Methoden besonders wichtig für das Verständnis kooperierender Eigenschaften wechselwirkender Teilchen sowie für die Simulation von Vielteilchensystemen.

(1.1) In einem idealen Kristall sind alle Atome regelmäßig im Kristallgitter angeordnet. In der Regel werden wir allerdings keine perfekten Anordnungen vorfinden.

Das Perkolationsmodell ist ein einfaches Modell zur Beschreibung eines ungeordneten Materials. To percolate bedeutet "Durchsickern": Wir beschreiben ein poröses Material, durch das gewisse Teilchen hindurchdiffundieren sollen, falls durchgehende Wege durch die Poren existieren

Wir werden im folgenden das Perkolationsmodell vorstellen und simulieren.

(1.2) Wir gehen von folgendem Modell aus:

• Legierung mit zwei Atomsorten A und B
• die Konzentration der A-Atome sei p
• beide Teilchensorten sind gleichmäßig verteilt
• A-Atome besitzen kurzreichweitige magnetische Wechselwirkung
• Keine Kopplung zu B-Atomen: Kristall kann nur dann eine magnetische Ordnung haben, falls er ein unendlich großes Netz von zusammenhängenden A-Atomen besitzt.

Hinweis: Phasenübergänge gibt es prinzipiell nur in großen Systemen mit hinreichend großer Vernetzung, wir werden allerdings auch für endlich große Systeme bei einer kritischen Konzentration Anzeichen eines Phasenübergangs erkennen können.

Entscheidend ist die Größe der Strukturen der A-Atome, die untereinander verbunden sind. Eine solche Menge von A-Atomen, die durch ihre Kopplungen verbunden sind, nennen wir Cluster.

Bei kleinen Konzentrationen p wird es nur eine Menge kleiner Cluster geben und damit keine magnetische Ordnung. Mit wachsendem p wird die mittlere Größe der zusammenhängenden A-Atome ebenfalls wachsen, bis sich ab einem kritischen Wert p_c ein Cluster durch den ganzen Kristall ausdehnt.

p_c heißt Perkolationsschwelle oder kritische Konzentration. Für p > p_c koexistiert der unendliche mit vielen kleinen Clustern; erst bei p = 1 sind alle Plätze mit A-Atomen besetzt.

Für den unendlich ausgedehnten Kristall gibt es nur einen wohldefinierten Wert für p_c:

• Quadratisches Gitter mit 4 nächsten Nachbarn: p_c = 0.59275(3)
• Dreiecksgitter mit 6 Nachbarplätzen: p_c = 0.5 (exakt)

Diese Perkolationsschwelle hängt zwar ab vom Gittertyp und der Reichweite der Wechselwirkung, nicht aber von der speziellen Realisierung der Probe, wenn man die Kristallgröße gegen unendlich gehen läßt.

Hinweis: Im endlichen Kristall gibt es natürlich nur eine Wahrscheinlichkeit W(p) dafür, daß ein Cluster existiert, der zwei gegenüberliegende Seiten verbindet.

• Wert von p_c für verschiedene Gitterstrukturen und Clusterdefinitionen
• Mittlere Ausdehnung x(p) für p ® p_c
• Clusterwachstum oberhalb der Perkolationsschwelle
• Verteilung der Clustergrößen
• Struktur des unendlichen Clusters bei p_c

(3.1) Mit Def.

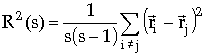
ist die mittlere Ausdehnung eines Clusters mit s Teilchen durch

gegeben, á …ñ _s<¥ bezeichnet den Mittelwert über alle endlichen Cluster.

x divergiert an der Perkolationsschwelle, und dicht bei x gilt:

was man für alle Perkolationsmodelle erhält. n ist universell: der Wert hängt nur von der Raumdimension ab:

• Bekannt in der Ebene für verschiedene Gittertypen und Reichweiten
• In realen zweidimensionalen Legierungen: n=4/3 (exakt)
• Drei Dimensionen: n=0.88 (numerisch)

(3.2) Die Wahrscheinlichkeit P(p), daß ein beliebig herausgegriffenes A-Atom zum unendlichen Cluster gehört, ist null bei p < p_c, und wächst stetig von P(p_c)=0 bis P(1)=1 an. Dicht bei p_c wird der Anstieg wieder durch ein Potenzgesetz beschrieben:

(bei p t p_c)

In zwei Dimensionen hat man: b=5/36 > 0.14, P(p) wächst also bei p_c sehr steil an.

(3.3) Direkt an der Perkolationsschwelle verschwindet zwar die Dichte des unendlichen Clusters (P(p_c)p_c=0), trotzdem existiert er und hat eine fraktale Struktur.

Die fraktale Dimension D eines Objektes ist gegeben durch M µ L^D, wobei M die Masse der es ausmachenden Elemente, und L seine Ausdehnung angibt.

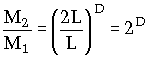
Beispiel: Betrachte die Massen zweier gleichartiger Würfel mit Kantenlängen L und 2L:

Wo D=3, bei Quadraten offensichtlich D=2 und bei Strecken D=1.

Man hat ferner:

Unterziehen wir nun einen quadratischen Ausschnitt unseres unendlichen Clusters mit Kantenlänge L und M(L) Teilchen in diesem Ausschnitt einer Untersuchung, so haben wir bei p_c:

wobei man den Mittelwert über verschiedene Ausschnitte betrachtet. Die Masse des Clusters wächst mit einer Potenz der Länge, und in der Ebene gilt D=91/48 > 1.89.

(3.4) Neben den drei Potenzgesetzen mit den universellen Exponenten n, b und D werden noch weitere Eigenschaften von p_c durch solche Gesetze beschrieben, die nicht unabhängig voneinander sind. Diese Abhängigkeit wird durch Anwendung der Skalentheorie deutlich.

Wir wollen diese kurz nachvollziehen: Wir messen L in Einheiten von
(p–p_c) oder x, sowie M in Einheiten von x ^x:

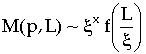
Setzen wir L=k x mit k=const., so folgt x=D. L wird also in Einheiten von x gemessen, M in Einheiten von x ^D. Wir skalieren die Meßgrößen in Potenzen einer gewählten Einheit, daher der Name Skalentheorie.

Aus L=k x folgt auch:

wobei L^d die Anzahl der Gitterpunkte im d-dimensionalen Würfel mit Kantenlänge L ist. M/ L^d ist aber die Wahrscheinlichkeit, daß ein Gitterplatz zum perkolierenden Cluster gehört. Für große L-Werte gilt daher:

und:

Daraus schließt man: b = (d – D) n . Die drei kritischen Exponenten sind also durch ein Skalengesetz verknüpft.

4 Finite size scaling

(4.1) Diese Exponenten sind nur für ein unendlich großes Gitter definiert. Wir arbeiten auf dem Rechner mit endlichen Gittern. Hier gibt es folglich keine Divergenzen, keinen Phasenübergang, keine scharfe Perkolationsschwelle. Mittels der Theorie des finite size scalings ist es möglich, vom endlichen System auf die Gesetze des unendlichen Systems zu schließen.

Die Konzentration p und die Systemlänge L sind in der Nähe von p=p_c und L=¥ miteinander verknüpft, und zwar vermittels

D läßt sich aus der Gleichung von Seite 4 oben numerisch ermitteln, für L ` x sieht ja das endliche System wie das unendlich große aus. Man kann also mittels M(p_c,L) ~ L^D den Exponenten D bestimmen.

Nun benötigen wir noch p_c und n . Hierzu führen wir die Wahrscheinlichkeit p (p, ¥ ) ein, daß es in einer Probe der Größe L einen Cluster gibt, der perkoliert:

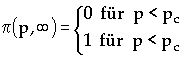
Wir stellen wieder eine Skalengleichung auf, die analog zu der für M(p, L) aufgebaut sein soll. Der Skalenexponent hat den Wert 0, da im Unendlichen p eine Konstante ist:

Wir besetzen also die Plätze im Gitter mit der Wahrscheinlichkeit p mit Atomen. Für p® p_c wachsen die Cluster, bis bei p_c(L) ein perkolierender Cluster auftreten wird.

Die Wahrscheinlichkeit, daß p_c im Intervall [p, p+dp] liegt, ist durch (dp/dp)dp an der Stelle p_c(L) gegeben. Das Maximum von dp/dp divergiert für L® ¥ , wobei es zur Perkolationsschwelle p_c des unendlichen Gitters hinläuft. Numerisch ist dieses Maximum nur schwer bestimmbar; besser ist es, Mittelwert und Abweichungen von p_c(L) zu bestimmen:

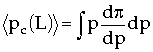
Man erhält hierfür mittels der Skalengleichung folgendes Skalengesetz:

Daraus folgert man mit z = (p–p_c) L^1/n und ò (dp/dp)dp = p(1, L) – p (0, L) = 1:

Wir bestimmen für viele Simulationen eines Systems mit möglichst großem L den Wert p_c(L). Damit können wir den Mittelwert á p_c(L)ñ bestimmen, was uns p_c und n liefert.

(4.2) Mit Hilfe der Skalengesetze können wir also die kritischen Werte des unendlichen Gitters aus den Eigenschaften endlicher Systeme berechnen. Das Werkzeug des finite size scalings ist übrigens nicht nur auf das Perkolationsproblem anwendbar, es gilt vielmehr für alle Arten von Phasenübergängen, und stellt ein wichtiges Hilfsmittel dar, um universelle, also modellunabhängige Größen zu berechnen.

5 Implementierung

(5.1) Erzeugung der Perkolationsstruktur auf dem Gitter: Wir benutzen gleichverteilte Zufallszahlen r Î [0, 1].

Das Ergebnis ist eine scheinbar regellose Struktur, deren Auswertung allerdings weitaus schwieriger ist, als ihre Erzeugung.

Die Frage, ob solch eine Struktur perkoliert oder nicht, läßt sich nicht leicht beantworten. Unser Auge ist mit der Beantwortung überfordert. Perkolation bedeutet hier anschaulich: Es gibt hier also einen Weg über besetzte Nachbarplätze, der zwei gegenüberliegende Seiten verbindet.

(5.2) Wir benötigen einen Algorithmus, der Cluster von zusammenhängenden Teilchen identifizieren kann. Eine elegante Methode dazu schlugen Hoshen und Kopelman (1976) vor: Das Gitter wird einmal durchlaufen, und an alle besetzten Plätze werden Clusternummern vergeben. Jeder Platz, der nicht mit einem vorher besuchten verbunden ist, bekommt eine neue Nummer

Unser Algorithmus basiert auf einem Vorschlag von Leath (1976). Wir erzeugen Cluster direkt im Wachstumsprozeß. Nur das Zentrum eines zunächst leeren Gitters wird besetzt. Alle Nachbarplätze, zunächst weder als besetzt noch als unbesetzt definiert, werden gemäß der Wahrscheinlichkeit p besetzt, bzw. unbesetzt gelassen. Dieser Prozeß wird iteriert, wobei jeweils alle noch undefinierten Plätze als besetzt oder unbesetzt definiert werden. Existieren keine undefinierten Randplätze mehr, wurde ein Perkolationscluster erzeugt.

Viele Wiederholungen ergeben eine Verteilung von Clustern, die man mit Methoden des finite size scaling auswerten kann.

Da jedes erzeugte Teilchen das statistische Gewicht p bzw. jede Leerstelle (1–p) erhält, und der gesamte Cluster mit dem Produkt aller dieser Faktoren gewichtet wird, erzeugt der Wachstumsprozeß die Cluster mit derselben Wahrscheinlichkeit, wie die vorherigen Algorithmen.

(6.1) Wenden wir den unter (4.1) skizzierten Algorithmus auf ein Quadratgitter der Kantenlänge 500 an der Perkolationsschwelle p=0.59275 an, so erhalten wir das in Abbildung 1 dargestellte Ergebnis: Schwarze Punkte repräsentieren A-Atome. Aus dem scheinbar regellosen Rauschen lassen sich kaum Gesetzmäßigkeiten erkennen.

(6.2) Abbildung 2 hingegen zeigt einen mit dem Wachstumsalgorithmus aus (4.2) erzeugten Cluster, der mit denselben Eingangsparametern arbeitet (Kantenlänge, Konzentration), wie der für Abbildung 1 verwendete. Der Cluster zeigt Strukturen auf allen Längenskalen, er ist ein fraktales, selbstähnliches Gebilde.

Man beachte, daß natürlich nicht immer perkolierende Strukturen erzeugt werden: Sehr oft stoppt der Wachstumsprozeß, bevor der Cluster den Rand erreicht hat.